今後の記事の内容について

いかに古典的な素材を話題にしているかがわかろうというものですが、 「集合被覆」の話は初回とその続編の間にじつに一年以上が経過してしまいました。

このような「最適化の実例」の記事は読んで頂いている方々の 手元で最適化ツールの動作を具体的に見ながら動作を実感して頂くのが最も良いのですが、 この媒体では私が関わっている商用最適化ツールのサンプルを配ることはできません。 結果だけ見せるこのスタイルでは結局言いたいことがあまり伝わらないかもしれない、 という考えでしばらく更新をためらうこととなりました。

つきましては、 このブログがこれまで主要な話題としてきた「最適化を実例を通じて示す」については、 その商用数理最適化ツールのページにあるブログに譲ることにしたいと思います。 こちらは商用ツールを離れて書きたい話題が出たら更新します。

ここまで本ブログにお付き合いいただき、誠にありがとうございました。

「習うより慣れろ」で始める数理最適化:「集合被覆」の例題（２）

車両 1 ～ 5 と、それらが巡回する部品工場 A～F の対応は同じで、今度は下の表が示すように毎日、 消耗品を所定のケース数だけ届けねばならない、という状況を考えます。

前回のように「とにかく届ければ(車が行きさえすれば)よい」というわけではなく、 車両にも積載量の上限（それぞれ80ケースとします）があると考えます。 結果のイメージを Excel を使って作ってみましょう。

肌色のセルに値を入れて、タテ計が需要に揃うように、 ヨコ計が車両の積載量の上限 80 を越えないようにすればよいのです。 Excel の式を定義しておけば、セルの値を入れるとタテ計とヨコ計が一瞬で更新されるのはよいのですが、 計画を立てるというのは、結局 ５（車両）× ６（工場） = 30 個のマスに値を「手で」入れてゆくことに他なりません。 値の組み合わせはそれなりに膨大なので、何か指針が要ります。 前回の最適化結果によると、車1と車4 に頼めばとにかく全部回り切れる。 ただ、

のように車１と車４だけで運ぼうとすると、車１の容量オーバー。 確かに需要量合計が 170 ケースで二台分の容量をわずか超えてますので車３台が必要な理屈です。 安易ですが工場C をカバーしてくれている車 3 を使って

という感じで結果を一つ導くことができます。

では、Excel の数式相当の情報を数理モデルとして食べさせて、 数理最適化に集計値になるようなセルの値を「逆算」してもらいましょう。 積載量を守り、需要を満たす範囲で使用する車の台数をできるだけ少なくしなさい、とすると

という答が出ます。 車１、車４ で運ばせることを軸として手で作った答とずいぶん様相が違うのですが、 ちゃんと制約は満たせていて、どうやら 3 台で運ぶ方法は一通りではないらしいとわかります。 最適な方法というのは一つしかないような気がするものですが、実務的の問題で答が沢山あり得る状況はむしろ普通です。 パズルを解くようにしてたった一つの答を探しあてる、というよりも沢山のあり得る答の中から気持的にしっくり来るものを絞り込んでゆく。それこそが実務の現場における数理最適化の醍醐味とも言えます。

まず、各車が実際に運んでいる量を見ましょう。最初に作った車1,3,4 を使う 結果も、数理最適化が出した車1,2,3 を使う結果もどうにもバランスが悪い。 最も運ぶ量が少ない車は最大積載量の半分も運んでいません。 各車の最低積載量が 50 という制約を付けて、最適化に再度探索させてみましょう。

全然違う車両の組みあわせ車５を使って 車両の負担は同じような感じの結果が出ました。 でも、ちょっと待ってください、 工場 A の需要 40 を車1と車5 の二台でまかなうようになってしまっています。 到着が前後したりすると品物を受け入れる工場側の手間は増えます。 一工場に対して担当車両は一つにまとめましょう。 それには、車両の台数の他、肌色のマス目で 0 以外が入っている個数をできる だけ小さくしなさい、という目的関数を加えます。次が出てくる答の一例です。

あれあれ、工場Ａを担当する車両は一台になりましたが、今度は工場B の担当がばらけていて、 結局値が書いてあるマス目の数は変化していません。

最適解がこれだということは、そもそも最低積載量が50 で、 一顧客に一台の車両、という答があり得ない、ということを示しています。 所望の答を得るためには、制約を緩めるしかありません。 50ケースという最低積載量がきつかったようなので、45ケースとしてみると、 無事一つの車両が一つの工場を担当する結果となりました。

実務の世界では、このようにそもそも答が存在するかどうかわからない問題を解くことは普通です。 数理最適化はうまく使うとこのように全体を見通した知識で膨大な試行錯誤からユーザーを開放し、 問題と「対話」するように結果に迫ることができます。

「習うより慣れろ」で始める数理最適化:「集合被覆」の例題

車両 1～5 と、部品工場A ～ F との対応を示している表があります。 どんな状況が想定されるでしょうか？

ここはあるメーカーの本社組み立て工場。 操業には部品工場(A～F)からの部品を仕入れて来る必要があって、 この表は仕入れをしている 5台の車のそれぞれが、 今日、仕入れ先のどこを回ることになっているかを示しています。なぜこの表が必要になったかというと、 急ぎで今日中に各部品工場すべてに届けたいものが生じたのです。仕入れのついでに持っていってもらうことにしようと思いますがどの車に頼めば、すべての部品工場を網羅できる(カバーできるか）か決めたい、とします。 すべての部品工場を網羅している車はないので、複数の車に頼む必要がありますが、できるならば最小限の車に頼むことで済ませたいのです。

この問題は「集合被覆問題」というなかなか使いでのある数理最適化の例題になるので Excel を入口にして、数理最適化という道を辿ってみます。 まず、どの車に頼むかどうかの選択をセルに入力すると、部品工場がカバーできるかがわかる、という表を作りましょう。以下はイメージです。

さて、これを例えば Excel で作るにはどうすればよいかです。方法は一つではないですが、○×のままだとしんどい。文字を数字に置き換えて、Excel の数式が使えるようにする案が定番として浮上します。慣れている方ならば、元の表と連動させて、次のような表を新たに作ることは造作もないことかと思います。 具体的には、黄色のセルに、各車両に実際頼むかどうかを 0-1 で入れ、IF 関数を使って、○を 1 で、空白セルを 0 で置き換え(オレンジの部分)、緑のセルには SUMPRODUCT を使って、各工場がカバーされたら 1 以上の値が入るようにしておきます(下図)。

黄色のセルを変化させると、緑のセルの値が瞬時に変化するはずです。 ま、実際この程度ならばこの表を見ながら試行錯誤するので十分ですが、せっかくですから数理最適化で「逆算」してみましょう。逆算とはすなわち数理最適化に、黄色のセルに１が入る数（車両に頼む数）を最小限にとどめつつ、緑のセルの値がすべて1以上の値になるようにします。

ここからは数理最適化ソフトが必要になります。それぞれ固有のやり方を覚える必要がありますが、黄色のセルを「変数」と定義して、緑のセルに定義されている数式を制約、黄色のセルの和を目的関数として教えます。 数理最適化ソルバーが導いた答は次です。

車1と車4に頼めば無駄なく（緑のセルに１が丁度入る）回ることができることがわかります。Excel 技を使って、元の○×の表に結果を書き込んでみましょう。

「数式臭さ」が抜けて、普通に人に見せてわかる、イメージした通りの表になっています。途中は○とか×を 1 と 0 に置き換えて途中の計算をわざわざ数字にしていました。これを理屈っぽく言うと「数理モデル化を行った」ということになりますが、これはつまるところ、Excel の数式を使うためで「便利」だからにすぎません。数理最適化でも同じ事情です。数理最適化でむやみやたらと数式に頼った記述は避けるべきと私は思っています。黄色のセルにはあくまで 0 か 1 しか入れることができず、0.4 とかいう値は入れられません(頼む、頼まないの二択なのに、意味が変になりますよね)。こういう変数を離散変数( 0-1 変数 ) と呼び、字義通り 0 とか 1 という意味ではなく、モデルの作り手により '○' とか'×' という意味を付与されています。

前回は「生産量」、という量そのものを変数にしましたが、実際の意思決定の場面では、このように「やる/やらない」とか、「どれを選ぶ」とかを決めることも多く、そこから現れる、離散変数を含む数理最適化問題は数理最適化の一大研究分野となっています。

今回は、「急ぎで各部品工場すべてに届けたい」という、突発的なニーズに対応しましたが、次は同じ表から出発して定常的なニーズに対応したモデルにしてみましょう。

「習うより慣れろ」で始める数理最適化:「生産計画」の例題 (2)

前回は Excel による集計表をベースに数理最適化のモデルを記述して、

という表を得るところまで進みました。 丸で囲った「生産量」のところの数字が数理最適化の答です。 タイトル通り、面倒な解説は抜きで、どんどん数字を変えて数理最適化の応答を見てみましょう。 製品 A,B に対して同じ利益というのも面白くないので、適当に A は B の 2 倍の利益という設定にしてみます。

利益は 80 とぴったりですが、 製品 A,B の生産量はなんだか微妙な数の答が出てきました。 在庫残りも絶妙(?)に調整されている風な値です。 製品Aの生産量、どうにも半端な 34.7 を 30 に切り捨ててみましょう。

利益は減るところからみて、たぶん先ほどのは最適解だろうとは思うのですが、試みに製品Aの生産量を30のまま、残り原料在庫で製品Bを作れるだけ作ることにするとどうでしょう。 原料 q に着目すると (320-8×30)/4 = 20 だけ作れます。書き込んでみましょう。

おっと、数理最適化の出した「最適解」と同じ利益 80 の解がもう一つ作れてしまいました！ 実はこの場合、製品 A,B が原料 q を使う比率(8:4=2:1)と利益の比率(2:1)が一致しているので、一旦利益 80 の答を得てしまえば、原料 q を使い切るように比率を保ったままA,B の生産量を操作すれば、「最適解」が量産できてしまいます。 製品 A だけ作って原料 q を使い切る答もありそうです。320 / 8 = 40 作ればよいわけです。入れて確かめてみましょう。

これでも利益 80 が得られます。 一般に数理最適化ソルバーが「最適解」だと言って答を返してきたからといって同等に良い答が他に存在しない訳ではないことにどうかご注意ください。言えているのはこれ以上良い答が存在しないことのみで、同等の答がこうして沢山あるのは実務的な数理最適化モデルを試行錯誤しているときには決して珍しいことではありません。

このような場合には「最適」の定義を見直してみましょう。上で示した３通りの答の原料の残り方を見てみます。最初に数理最適化が出した答 (製品A,製品B) = (34.7,10.7)だと

(製品A,製品B) = (30,20)だと

(製品A,製品B) = (40,0)だと

実現されている利益は同じ 80 でも、こうして残り在庫を見ると決して等価な答とは言えません。「最適」の尺度が「利益」だけ、と単細胞なのでその実現方法は沢山あり、その結果として多くの「最適解」が出現してきてしまったのだとも言えます。そもそも残せばよい原料の在庫は数理最適化が「全自動」で決めるべきものではありません。今後の需要予測に基いて人間が行うものであり、数理最適化は人間のポリシーに従って実現値を導く役回り（意思決定の補佐）を振られるのが一般的です。試しに利益を固定して、原料r の在庫残りが 25 になるようにしてみましょう。実験は数理モデルを若干改修すればよいので実に手軽(数式表現が気になる方へ: 利益を 80 に固定し、原料rの在庫残りと 25 の差の絶対値を目的関数にします)。

丁度合わせてきました。では、在庫残り 30 ではどうか？

これでもぴったり合わせて来ます。 こうしてモデルが出す便宜上の「最適解」を見ながら、人間が対話的に条件を設定して結果を絞り込むのが数理最適化の実践的な使い方です。あれ、と思ったら人間が結果を打ち込むこともできる。これはまさに Excel の使いどころではないでしょうか。

次回はこの表の構造は同じまま数を拡張して別の問題にしてみましょう。 　　　　　　　　　　　

「習うより慣れろ」表計算で始める数理最適化:「生産計画」の例題 (1)

「数理最適化は表に始まり表に終わる」というのは私が勝手に作った言葉ですが、 我々が普通に Excel などを使って作る集計表を数理最適化にかけると、集計結果が意図した感じになるよう都合良く数字を書き込んでくれたりします。ここから始まるちょっとしたシリーズでは表計算から最短コースで数理最適化の本質(の端っこ)に迫ってみます。

製品を2つ作れるとして、それぞれは 3つの原料を決まった量だけ使います。各製品を単位あたり作ったときの利益と原料の在庫の表が次のように与えられています。製品は A,B 、原料は p,q,r としています。

製品 A を 1 単位作ると原料 p,q,r をそれぞれ 4,8,1 消費して、利益が 1 出ます(表を横に見る)。 製品 B も 1 単位生産で利益 1 を得ますが、所要する原料は微妙に異なっています。原料在庫も表に加えておきました。

さて、この表をちょっと拡張して製品の生産によって消費される原料の量や利益の欄を加えます。Excel の数式や関数を使って、オレンジのセルに値が入力されたら緑のセルに数字が出るようにしてみましょう。

足し算と掛け算でもよいですし、"SUMPRODUCT" なら、なお簡単。 「生産量」を示すオレンジのセルについては絶対参照をうまく使うと簡単ですね。。 とかいうのはこの Web 上に溢れる Excel 関連の情報源を辿って頂くとしましょう。

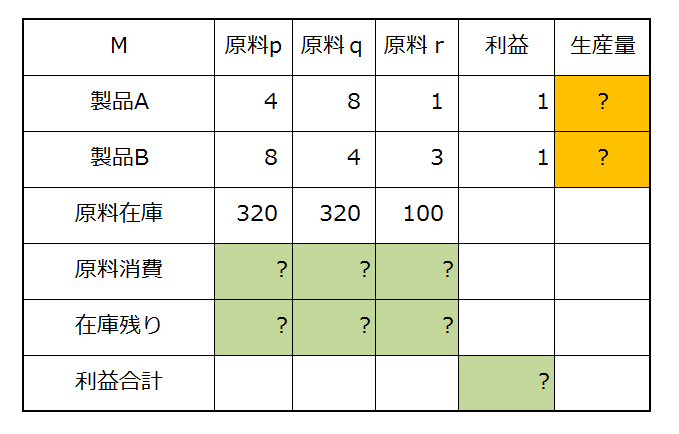
できました。次は A,B の生産量の欄に 5,6 と適当に入れた場合の表の値です。 在庫はまだ余裕で利益は 11。

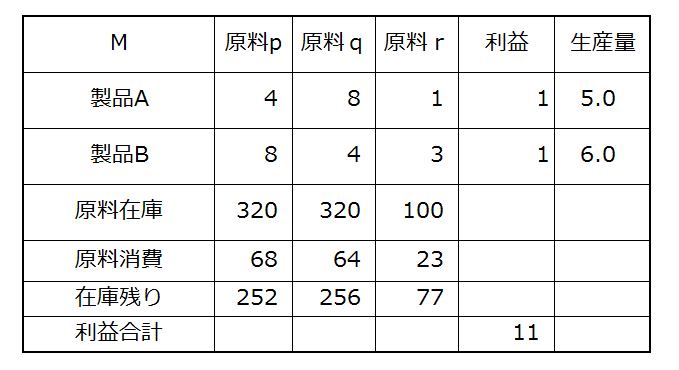
「生産量」のセルをあれこれ触ると利益とか在庫残りがリアルタイムに変化します。 A の生産量を 7 にすると。。

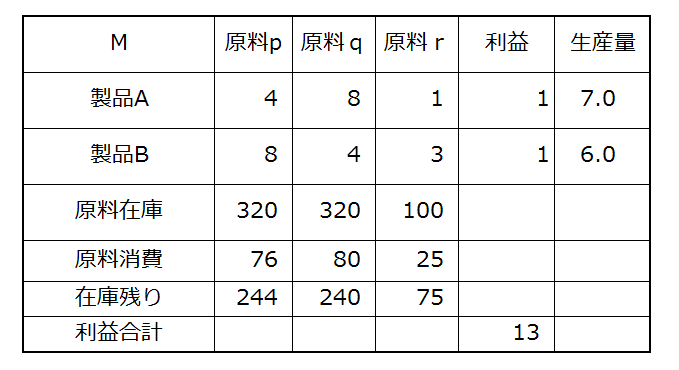
利益がちょっと増えましたね。もっと増やすにはどうしましょう。 原料在庫が許す限り生産すればよいのです。 まだ余裕ありそうですので、思い切って 30 ずつ作ると、

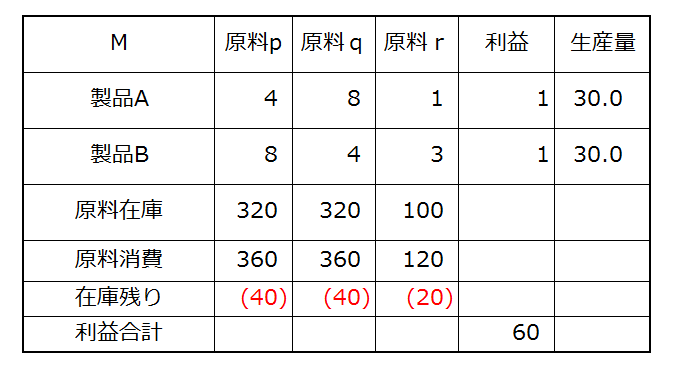
あれあれ在庫をショートしてしまいました。これでは使えません。もうすこし減らして良いところを探りましょう。。

数理最適化を実感する上でこんなに良いツールはない、と良く思います。 これはただの Excel 演習で全然数理最適化じゃないだろうって？ 確かに。でも我々が数理最適化にやらせているのはこの「生産量」セルの値についての試行錯誤の肩代りであり、Excel をはじめとする表計算は数理最適化ソルバーの操作を実演し、実感する格好のツールなのです。

さてここからは数理最適化ソフトが必要で、各ソフト固有のやり方を覚える必要がありますが、 数理最適化ソルバーに、何をすべきかという「ゲームのルール」(数理モデル)を教えるのは、このExcel 上で SUMPRODUCT とか使って数式を定義する操作とやっていることは本質的に変わりません。数理最適化ソルバーに、変数は「生産量」のセルの値であるということ、「生産量」セルの値を使って在庫残りは 0 以上でなくてはならないという制約を定義し、利益を最大化したいのだ、と教え込むことができたとしましょう。解かせてみます。 数理最適化ソルバーの答が返したのは 製品A,B をそれぞれ 28,40 作る利益 52 の計画でした。

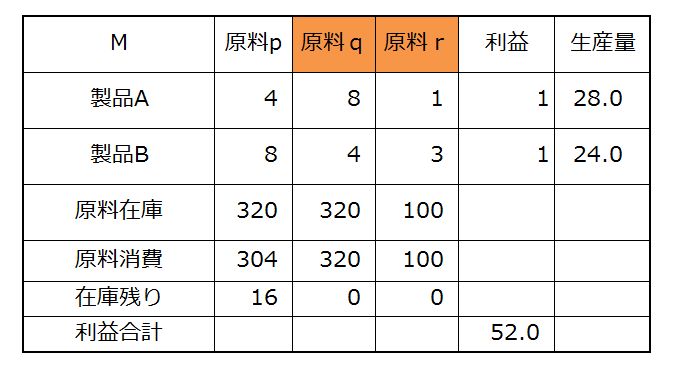
ご存知の方も多いと思いますが、じつはこの例、 数理最適化の教科書の「導入」の定番なのです(ふと思い立って私の周りにある本、和洋とりまぜて 11冊を調べてみたら、じつに 8 冊がこの例題に類するものを導入に使っていました)。 ただ A,B = 28,40 という、一つの結果から得られる情報には限りがありますから、 教科書の書かれた頃よりもおそらくは恵まれた計算機環境を手にしている、というアドバンテージを活かし、数字をいろいろ替えて試しながら数理最適化というやつのお手並みを体感してみましょう。 ぱっと見わかるのは q,r の在庫を使い切る答になっているということ（表で使い切られた原料は色付けしています）。原料がすべて余っているならば製品にしてしまえばよいわけで、これは確かに妥当な動作である感じがします。では原料 r の在庫を 105 に増やしてみましょう。

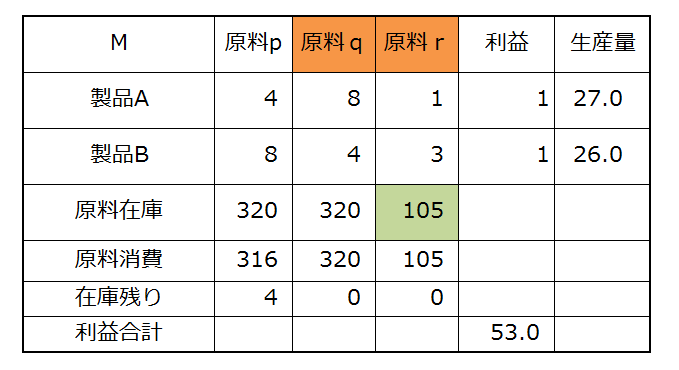
増やした r をまた使い切って 1 利益が増えました。 では思い切って r の在庫を 120 にしてみます。

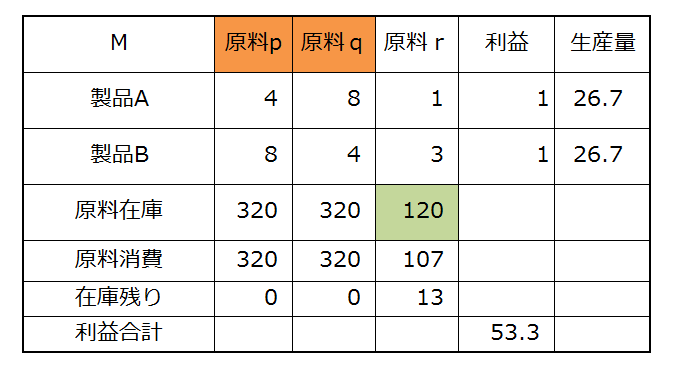
あんまり素直に利益は増えません。r を使い切ることができてません。 原料 p,q の在庫が使い切られているところを見ると、今度は p,q が頭打ちになっているのだなとわかります。 原料 q の在庫を増やしてみましょう。

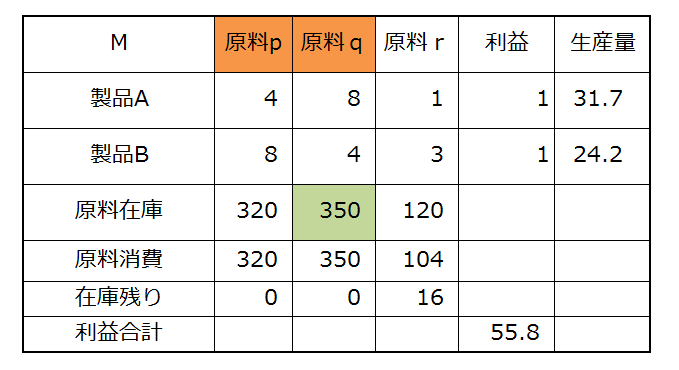
無事 q の在庫を使い切って利益を増やす答になっています。 こうやって試していると、(求めたかったはず)の生産量の値より、 どの在庫を使い切っているかというところから結果を理解する方が容易なことがわかります。 実は、数理最適化の教える知見の一つに、

  丁度満たされている制約(使い切っている在庫)によって答が決まる。

という事実があります。特に数理最適化が求めようとしている量の一次の式(定数倍の和)によって問題が表現されている線形計画法の場合、どの製品の在庫が使い切られているか、という情報は答の情報と等価である、とすら言えてしまいます。もちろんどの製品の在庫が使い切られているかを知るために目的関数を参照しているのですが、出てくる結果を陽に支配するのは制約式の方で、だから目的関数のウエイトをいじっても結果が付いてこない・・といったことが起きます。

教科書だと、次のような感じのグラフが出てきて

結果を「解析的に」(要するに筆算)で求め、 どうして最適と言えるのか説明したり、一般的な解き方を解説したり、さらには「双対変数」とかいうじつに不可思議な量の説明に入ってしまうのですが、じつは、こういう知識はツールとして実務的に数理最適化ソルバーを使い出す上では不要。 Excel 上に問題を表現した段階で、数理最適化を始める準備(数理モデル化)はもうできています。 「習うより慣れろ」でどんどん動かすことで、知見を得てゆきましょう。そうする中で教科書を読んだだけではわからない事実も見えてきます。

次回はこの生産計画のモデルをもうすこし触って、数理最適化の性質に迫ってみます。

数理最適化に意思決定ができるのか？

倉庫には容量以上の在庫は入らない。 納期を守るには先立って一定のリソースを割く必要があるし、 休暇は所定の数だけ必ず取ってもらわねばならない。 数理最適化はそんなビジネスの「ロジック」を取り出して記述し、 その枠内で良さげな答を探しださせる手法です。 しかしビジネスが「ロジック」だけで動いているかというと、さにあらず。 実務家はロジックの枠に「意志」とか「予測」とか「期待」を流し込んでゆくのが普通です。 時に彼らは問題の枠組みや制約を踏み外して、使える答をひねりだしてしまうことだってあります。

私も以前は好んで使っていたこういう宣伝文句

「(数理)最適化で意思決定！」

お聞きになったことありますでしょうか。 私の経験で言うといまいちで「意思決定」というワードがお客様の胸に響いたということはなかったように思っています。 数理最適化は自動化という言葉で括られる所作、 例えばエネルギーコストを最小化すべく動力プラントのボイラーの運転を決めたり、 レコメンドしたりといったいわば「マイクロ意思決定」は十分できているのですが、 新しい営業所を開いたり大規模な設備を増設したりといった人間が担当している重要な意思決定であるほど、ロジック以外の部分を無視することはできないので、数理最適化任せにできないという感覚をお持ちの方が多いということだと思います。

では、「ロジック」の権化である数理最適化は何もできないかというとそうでもなく、得意なその路線で頑張ればよい。

「もしこの設備を導入したとして最適に運転したとすると..」
「すべての人の休暇希望を叶えて、できるだけ残業を減らすには..」
「コストはさておいて生産性を最大にしてみると..」

数理最適化は恣意性が入らない、 誰もが認める「ロジック」を冷徹に突き詰めた答を出すことで、意思決定者の検討材料を増やすことができます。 シミュレーションとしての利用と言えるでしょうか。「最適にする」という一言でくどくどデータを与える必要がないのがメリット。

そんなわけで先のフレーズを言い直すと

「数理最適化で意思決定の脇を固めましょう！」

となるでしょうか。意思決定の裏方仕事ならちゃんとできることはわかってほしいなと願っています。

コンピュータの得意な部分をどうやって人間の仕事に組み込むのかという文脈で、 「アドバンスド将棋」に関する論考を見つけました。人によってコンピュータに任せようとする部分は様々なのも面白い。こういった考察はまだ初まったばかりなのだと感じました。人工知能に支配される暗黒の未来といったホラーな話よりもぐっと夢があって、わくわくする話であります。

「最適化」のち「数理計画法」再び「最適化」

「最適化」という言葉を Web で探すと

スマホ最適化、ディスク最適化、画像最適化・・

といった感じのものがひっかかってきます。 「今よりも良い状態」を実現する手段といったニュアンスですね。 じつは学術的な数理最適化の分野の「最適」はもっと杓子定規に定義されているのをご存知でしょうか。研究論文とかでは、制約を満たすだけの答は「実行可能解」という格下の名前で呼ばれ、今得られているよりも目的関数値を良くする実行可能解が存在しないことを「証明」できて初めて最適解に昇格するのです(だからでしょうか、最適解は x* とか星を付けて「偉さ」を示すのが慣例)。 ですので、厳密解法という、いつかは最適解を出力することを謳っているアルゴリズムではそれよりも良い実行可能解が存在しない証明にかなりの労力をかけます。 その意義はここに示した通りですが、難しい問題だと答は見つかってるのに延々と「証明」を続けてメモリを使いつくしてしまったりする。それではあまりに悲しいし、とにかく制約を満たす方法だけ知りたい場合もあります。

そんな融通の効かないこと言ってないでそこそこ良い解を速く出そうよ

という発想が「近似解法」という、厳密解法に対置される一つの解法の流れを進化させてゆきました。 じつはこちらの方が「最適化」という言葉の一般の意味に近いとも言えます。

実務に数理最適化を応用しようとする中、我々がお客さまと話す中で気づいたのは

「最適」は一つに定まらない

という悟りです。世の中には各人が自分の好きに解釈できる程度に曖昧なので、 なんとなく意思の疎通が取れたような気になってしまう言葉がありますが、 実は「最適化」はその代表格。「最適化しよう!」という点では仲良くしてたのに何を優先するかの各論に入ると途端に対立して話がまとまらなかったりする担当者の方々が居たり。 まあまあ、まずは今より良くしましょうよ、という感じでスパイラルに話を進めるのが我々の数理最適化の実務における常套的プロセスになっております。

一時期のことですが私、「最適化」という言葉の曖昧さが嫌で「数理計画法」という言葉を好んで使っていた時期があります。この時期に私が書いた資料のタイトルが、

 「最適化読本」-数理計画法って何なのさ-

となんだかわけがわからなくなっているのはそんなわけです。 「数理計画法」なら数理的なルールをモデルで抽象化して表現して何らかの答を見出す手法をあまねく指す言葉ですから、曖昧さがない。 ただ、なんだかとっつきにくいし、一回聞いただけでは頭に入りにくい。

近似解法を使ってシフトスケジュールなんかを求めているのは、 じつは学術的な最適化ではなく、「スマホやディスクの最適化」に近いんだから、 名実共に我々は一般の意味の「最適化」をやっていると言ってもよいのではないかな、と今は考えています。